PEP 6305 Measurement in
Health & Physical Education
Topic 5: The
Normal Distribution
Section 5.3
 Click to go to
back to the previous section (Section 5.2)
Click to go to
back to the previous section (Section 5.2)
Hypothesis Testing
n
The complement to the
level of confidence is the
error
probability, which is equal to [100% – (level of confidence)]/100.
n
In terms
of the sample mean, the probability of error tells you how often the confidence interval does not include the population mean: in other words,
how often that you would be
wrong to make that inference.
¨
In this way,
probability of error is central to hypothesis testing
(Topic 8
discusses this in more detail, but some of the hypothesis testing concepts
related to probability and the normal distribution are relevant now).
n
In the context of hypothesis testing, error probability is called
α (the
Greek letter alpha), and represents the probability that the analysis supports the
research hypothesis when that hypothesis is actually wrong and that
support is in error; thus, it is
called
error probability.
¨
The α value is established before the study; investigators
decide before collecting data how often they are willing to be
wrong.
¨
Typical α values are 0.05 (wrong in only 1 in 20
experiments) or 0.01
(wrong in only 1 in 100 experiments); these correspond to 95% and 99% levels of
confidence (see the formula above).
¨
When analysis of the data results in an error probability (p)
that is smaller than the α value, we conclude that the research hypothesis is
correct, knowing that we have some small probability that our conclusion is
wrong (see box at right).
n
In hypothesis testing, a statistic is computed from data and its
value is compared to the distribution of that statistic.
¨
The p value is the proportion of possible values for the
statistic that are equal to or larger than the computed statistical
value.
n
For example, suppose you do an experiment with N = 100 and obtain a sample mean of 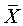 =
103 for a variable with a known population mean of 100 and population SD of 10.
Is your sample mean significantly larger than the population mean?
=
103 for a variable with a known population mean of 100 and population SD of 10.
Is your sample mean significantly larger than the population mean?
¨
Your
research hypothesis is that the sample has a higher
mean than the population. Your
null hypothesis is that the sample has the
same mean as the population. Both cannot be true.
¨
If the sample is part of the population, then 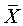 should
be
100 (the population mean), except for sampling error. The sample
value of 103 may just be due to sampling error. So, is 103 an unusually large
value? What is the probability of a mean this large occurring in a sample of
100 subjects in this population?
should
be
100 (the population mean), except for sampling error. The sample
value of 103 may just be due to sampling error. So, is 103 an unusually large
value? What is the probability of a mean this large occurring in a sample of
100 subjects in this population?
¨
If the value of the sample mean (103) has a probability (p)
of occurring in this population 5 times or less in 100 (α = 0.05) as a result of
sampling error alone, then we are willing to say that the sample mean is larger
than the population mean.
¨
One way to evaluate this is to find the critical value for an error probability
of
α = 0.05 (95% confidence).
·
Find the value for the 95th percentile: any value larger than that
value will occur in <5% of samples with N = 100. This 95th percentile value is
the critical value.
·
Find
the Z score for the 95th percentile: we need the Z score where 45%
of the scores lie between it and the mean; from Table A.1 or Excel, this value
is Z = 1.645.
·
Rearrange the
Z
score formula using the
SEM (SD/√N= 10/√100 = 1.00)
instead of SD to solve for X (we know
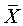 ,
the SD, N, and just found the Z we need): X = (Z × SEM) +
,
the SD, N, and just found the Z we need): X = (Z × SEM) +
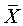 .
.
·
For our study: X = (1.645 × 1) + 100 =
101.645. This is the critical value; any mean larger than this would
occur only rarely (<5% of all samples of N = 100) in this population.
·
Since our sample mean (103) is larger than this value, we conclude that the
sample mean is larger than the population mean, with 95% confidence.
¨
We can also use a Z test to calculate the probability of 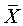 =
103 in this population. The "one sample Z test" divides the difference between
the sample and population means by the SEM (SD/√N = 10/√100 = 1.00):
=
103 in this population. The "one sample Z test" divides the difference between
the sample and population means by the SEM (SD/√N = 10/√100 = 1.00):
·
Z
= (X -
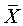 )/SEM
=
(103 - 100)/1 = 3.00.
)/SEM
=
(103 - 100)/1 = 3.00.
·
Find what percentile this Z score; (100% - percentile)/100 is the sampling
probability of this Z score.
·
The percentile for Z = 3.00 is 99.87% (Table A.1 or
Excel);
thus, the probability of a Z score of 3.00 is (100% - 99.87%)/100 = 0.0013. You
will often see this presented as "p = 0.0013".
¨
Interpretation: 99.87% of means from samples of N = 100 in
this population would be less than 103; thus, 103 is an unusually large mean.
¨
Since p < α (i.e., 0.0013 < 0.05), we reject the null
hypothesis (that the sample has the same mean score as the population) in favor
of our research hypothesis (that the sample has a higher mean score than the
population).
¨
The sample mean is said to be significantly larger than the
population mean. In scientific writing, the word “significantly” means ONLY one
thing: that the probability of an observed value of a statistic is very low when
compared to a known (population) distribution.
n
The concepts of levels of confidence/confidence intervals and
error probability exist for any sample statistic.
n
There is a tradeoff between error
probability and precision of the statistical estimate for a sample of a given
size.
¨
A very low error probability necessarily means that the estimate
is less precise, because a lower error probability corresponds to a
wider confidence interval.
¨
By contrast, a precise estimate (smaller confidence interval)
has
a higher error probability, making the estimate more likely to be wrong.
 Click
to go to the next section (Section 5.4)
Click
to go to the next section (Section 5.4)
![]() Click to go to
back to the previous section (Section 5.2)
Click to go to
back to the previous section (Section 5.2)

![]() Click
to go to the next section (Section 5.4)
Click
to go to the next section (Section 5.4)