PEP 6305 Measurement in
Health & Physical Education
Topic 10:
Repeated Measures
Section 10.1
n
This Topic has 2 Sections.
Reading
n
Vincent & Weir, Statistics in Kinesiology, 4th ed. Chapter
12 “Analysis of Variance with Repeated Measures”
Purpose
n
To demonstrate the comparison of measures repeatedly collected
from the same group of subjects using analysis of variance (ANOVA).
Repeated
Measures: Within Subjects Factors
n
Repeated measures research, in which the same measure is collected
several times in a single group of subjects, is very common in studies of
kinesiology and health.
¨
Pretest-posttest designs are one example, in which a measure
collected before a treatment is compared to the same measure collected after the
treatment.
n
Repeated measures designs are also called within subjects
designs.
¨
The repeated factor is called a “within” subjects factor because
comparisons are made multiple times ("repeated") “within” the same subject rather than across ("between")
different subjects.
n
Recall that
simple ANOVA
requires that the means being compared are
independent of one another.
When the subjects are in groups that are independent from one another, then
group is a between subjects factor.
n
Since repeated measures are collected on the same subjects, the
means of those measures study are dependent.
¨
A particular subject’s scores will be more alike than scores
collected from multiple subjects, meaning that there is less variability from
measure to measure than observed from person to person in simple ANOVA.
¨
Repeated measures ANOVA separates the
two
sources of variance:
measures
and
persons. This separation of the sources of variance decreases MSE,
the random variation (sampling error) component, because there are now two
sources of known variation (subjects and measures) instead of just one
(subjects) as in simple ANOVA. The variation in scores due to differences between subjects
is separated from variation due to differences from measure to measure within
a subject. (A smaller MSE increases
power.
Why?)
¨
Instead of comparing treatment effects to a group of different
subjects, treatment effects are compared across multiple measures in
the same subjects. Each subject provides their own "control" value for the comparison.
Consequently, this type of design is more sensitive to differences
(i.e., requires smaller differences in the dependent variable to reject
the null hypothesis) than are between subjects designs.
n
Repeated measures ANOVA requires different computation
than simple ANOVA. 
n
The repeated measures ANOVA null hypothesis is that the
means of the measures all have the same value. If the number of
repeated measures = k , the null hypothesis is:
¨
 ,
or the differences between the means of each repeated measure is equal to 0.
,
or the differences between the means of each repeated measure is equal to 0.
n
The statistic used in repeated measures ANOVA is F, the
same statistic as in simple ANOVA, but now computed using the ratio of the
variation “within” the subjects to the “error” variation.
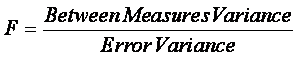
¨
The observed between measures variance is an estimate of
the variation between measures that would be expected in the population under
the conditions of the study.
¨
The observed error variance is an estimate of the variation
that would be expected to occur as a result of sampling error alone.
¨
If the observed (computed) value for F is
significantly
higher than the value expected by sampling variation alone, then the variance
between groups is larger than would be expected by sampling error alone.
·
In other words, at least one mean differs from the others enough
to cause large variation between the measures.
Repeated Measures
ANOVA Assumptions
n
The assumptions of repeated measures ANOVA are similar to simple
ANOVA, except that independence
is not required and an assumption about the relations among the repeated
measures (sphericity) is added.
n
Normality
¨
The dependent variable is
normally
distributed in the population being sampled.
¨
Normality of the dependent variable can be evaluated using a
histogram and
skewness
and kurtosis statistics.
n
Homogeneity of variance
¨
If there are separate groups of subjects in addition to the
repeated measure (within subjects) factor, then the variance of the dependent
variable in each group is equal (in the population).
¨
As in simple ANOVA,
homogeneity of
variance can be evaluated using a variety of statistical tests, but the most
straightforward method is to compare the within-group variances; one or more
variances twice as large as other variances may be a problem.
n
Sphericity
¨
This means that the variances of the repeated measures are all equal,
and the correlations among the repeated measures are all equal.
¨
This assumption is needed to allow for comparing the variances
among the repeated measures (within subjects).
¨
When evidence suggests sphericity is violated, the analysis is
adjusted. We’ll discuss this briefly
in
the next section.
“Within Subjects” Variance and “Error”
Variance

n
Means are computed for each measure (typically the
measures are in the columns of the data file) by summing across the
subjects and dividing by the number of subjects:
 where Xij is the score of a person (i) for measure j
and N is the number of subjects.
where Xij is the score of a person (i) for measure j
and N is the number of subjects.
n
Means are computed for each subject (typically the
subjects are the rows of the data file) by summing across the
measures and dividing by the number of measures:
 where J is the total number of measures in the study.
where J is the total number of measures in the study.
n
The grand mean is computed by summing across all measures and all
subjects and dividing by the total number of scores (N × j):
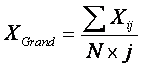
n
The between measures variance is the variation of the
mean of each measure from the grand mean.
n
The between subjects variance is the variation of the
mean of each subject from the grand mean.
n
The total variance is the variation of each score
(each measure for each subject) from the grand mean.
n
The error variance is any variation not accounted for by
the variation among the subjects and the variation among the measures.
¨
This "residual" variance = total variance – between
subjects variance – between measures variance.
Sum of Squares
n
Each component (Between Measures, Between Subjects,
Error/Residual, and Total) has a SS.
¨
Between Measures:
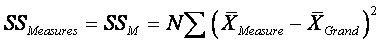

¨
Between Subjects:
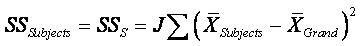
¨
Total:
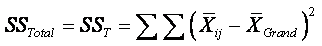
¨
Error/Residual:
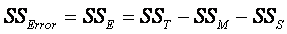
n
Each of these SS is a measure of
variability.
n
Repeated measures ANOVA compares the between measures
variability to the error variability using the F statistic.
n
Both SS measures are standardized by their respective
degrees of freedom,
creating Mean Squares.
Mean Squares
n
Compute the MS by dividing the SS by its respective
degrees of freedom (df).
¨
df = (the number of elements being summed in the SS) – (the
number of means subtracted in the SS)
¨
For each SS equation, compute the difference between the number
of elements ahead of the subtraction sign from the number of elements
behind the subtraction sign.
¨
dfW : How many elements are being summed in the SSM
equation above? The J measures’ means. How many means are subtracted from
these J means? 1—the grand mean is subtracted from the J means. So
dfM = J – 1.
¨
dfB : How many elements are being summed in the SSS
equation above? The N subjects' means. How many means are subtracted from
these N means? The grand mean is subtracted from the n means (in
each group). So dfS = N – 1.
¨
dfT : What is the df for SST? N × J
elements (all subjects and all measures) are summed, and then the grand mean is
subtracted, so dfT = NJ – 1.
¨
dfE : What is the df for SSE? dfE
= [dfT – dfM – dfS] = [(NJ – 1) – (J
– 1) – (N – 1)] = [NJ – 1 – J + 1 – N + 1] = [NJ – J – N + 1] = (N – 1)(J – 1).
n
Each component (Between Measures, Between Subjects, and Error) in
ANOVA has a MS : divide each SS by its df.
¨
Between Measures:
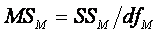
¨
Between Subjects:

¨
Error:
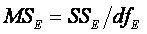
n
Compute F : 
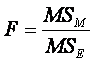 MSE represents the variation expected as a result of sampling
error alone.
MSE represents the variation expected as a result of sampling
error alone.
n
As in simple ANOVA, we compare the observed sample F value
to the F distribution to determine the likelihood that the value is due
to sampling error alone.
¨
If MSM is several times larger than MSE,
we conclude that the variation between measures is larger than sampling error.
In other words, the error probability (p-value) will be low, and we infer that
the measures are significantly different.
¨
The key difference between simple ANOVA and repeated measures
ANOVA is that the variation from measure to measure and the variation
from subject to subject have been removed from the
SSE in repeated measures, thus adjusting the SSE
(and MSE) for the within-subjects dependency of the measures.
 Click
to go to the next section (Section 10.2)
Click
to go to the next section (Section 10.2)


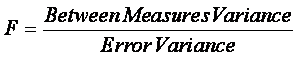

 where Xij is the score of a person (i) for measure j
and N is the number of subjects.
where Xij is the score of a person (i) for measure j
and N is the number of subjects.  where J is the total number of measures in the study.
where J is the total number of measures in the study. 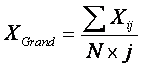


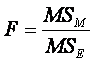 MSE represents the variation expected as a result of sampling
error alone.
MSE represents the variation expected as a result of sampling
error alone. ![]() Click
to go to the next section (Section 10.2)
Click
to go to the next section (Section 10.2)