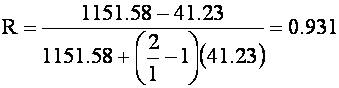PEP 6305 Measurement in Health & Physical Education

Topic 11: Reliability

Section 11.2

Click to go to back to the previous section (Section 11.1)

Intraclass Correlation

n   The method that we will use to compute a reliability estimate is called intraclass correlation.

¨  Intraclass correlation uses the MS values that are computed by analysis of variance (ANOVA).

n   Intraclass correlation can be computed using one-way (simple) ANOVA or two-way (repeated measures) ANOVA. The two-way ANOVA will be used in this course.

¨  The one-way ANOVA model is used if differences between the repeated measures are considered to be error--contrary to intuition, this is not always the case.

¨  If the F test of the repeated measures effect is not significant, the difference in reliability estimates between the one-way and two-way models is negligible.

¨  You will not be asked to compute reliability using one-way ANOVA in this course.

n   Calculating reliability is tedious to do manually, but is quite easy with a program such as LazStats. The approach in this topic will be to use LazStats to calculate ANOVA and illustrate the sources of the data.

n   Reliability Example 1 – Random Numbers

¨  This example uses a 4-trial fictional test administered to 7 fictional individuals. The test scores are random numbers, so the reliability should be approximately 0.

¨  The data set consists of a total of 28 scores, 7 subjects and 4 trials (7 x 4 = 28).

¨  Intraclass reliability will be illustrated using (two-way) repeated measures ANOVA of the 28 scores. Here is the resulting ANOVA table:

¨  The F value of 0.95 (p = 0.437) is very low, showing that the variance among the four trials is caused by chance variation: the trials do not differ.

¨  One equation for calculating intraclass reliability (R_xx) from a two-way ANOVA is:

R_xx = (MS People - MS Residual) / MS People = (4.57 - 2.85)/4.56 = 1.72/4.56 = 0.377

(this R_xx is the same as the intraclass correlation coefficient R₂ described by Vincent & Weir, p. 218, Table 13.4 Model 3,k--it includes only random error, the MS Residual, and does not include trial-to-trial differences, the MS Between Measures, as error. Other types of reliability include the trial-to-trial differences as error, such as when determining how closely raters agree (use Model 2,k from Table 13.4).

¨  The intraclass reliability of 0.377 is for a test score that is the mean of all 4 trials. (The effect of number of trials on test reliability is covered below.)

¨  Note, the 28 scores in this example are random numbers so the reliability estimate should be low and near 0. The reason that it is not exactly 0 is the sample size of 7 subjects is very small, so the sampling error is large. If we had a larger sample (> 50), the sampling error would be smaller and the value would likely be very close to 0.

¨  Assuming the intraclass reliability was actually 0.377, we can conclude the following:

·         The proportion of total variance, measuring true individual differences in whatever was tested, was 0.377 (37.7%).

·         The proportion of total variance that is measurement error is 0.623 (1.00 – 0.377 = 0.623), or 62.3%.

·         Thus, measurement error is much larger than true score differences. Reliability is low, and this is a poor test.

n   The purpose of this section is to illustrate the use of R Commander to estimate test reliability.

¨  This table provides actual leg strength data for a sample of 6 subjects, each tested 4 times, i.e., there were 4 trials. Download the ReliabilityEx file from Blackboard or right-click and "Save target as..." to download and save the ReliabilityEx file and import it into R Commander.

• Enter the following text into the R Commander Script window:

           ezANOVA(data=ReliabilityEx, dv=.(score), wid=.(subject), within=.(trial), detailed=TRUE) 

        n   Compare your output to the following:

·         Between Items F

·         The F value for the between-trials test is 1.214624 (p = 3.385 x 10^-1 = 0.339).

·         Indicates that variation among the means of the four trials is within chance.

·         Within People Total Variance.

·         The Within Total SS is the sum of the Between Items SS (31.125) and Residual SS (128.125).

·         The Residual MS = 128.125/15 = 8.542 (This is close to what you can compute to be the Total Within MS, 8.847, because the trials are not significantly different; hence, reliability estimates that do or don't consider trial to trial differences to be error would be essentially the same).

¨  Reliability Estimates

·         To compute this intraclass reliability coefficient from the ANOVA table values: 

R_xx = (MS Subjects - MS Residual)/ MS Subjects

= 282.88 - 8.542/282.88 = 274.338/282.88 = 0.970 

·         This is an intraclass reliability estimate for a score that is the sum/total of the 4 trials.

¨  Interpretation of the Reliability coefficient

·         Over 97% of the variance of strength test is due to true differences in strength among the subjects – some subjects are stronger than others and the test measures these differences.

·         Less than 3% of the variance of the strength test is due to random measurement error.

·         We can conclude that this is a highly reliable test.

Forecasting Reliability

n   The equation for forecasting test reliability with the ANOVA means squares.  

n   The terms are:

¨  MS_P = Between People Mean Square.

¨  MS_I = Residual Mean Square.

¨  k = number of trials administered.

¨  k' = number of trials for which you want to estimate reliability; this number will be either greater than or less than k, the number of trials actually measured.

n   Example: An arm strength test was administered to 207 people and there were two trials, resulting in the following ANOVA table.

n   Note the following information:

¨  Intraclass Reliability for two trials = 0.964 (How do we know this?)

¨  Data For Forecast Equation:

·                           MS_P = Between People Mean Square = 1151.58.

·                           MS_I = Residual Mean Square = 41.23

·                           k = number of trials administered = 2.

¨  Forecasting Reliability: For one trial (k' = 1)

¨  Interpretation - The reliability for the test if only one trial was administered would be 0.931, slightly lower than for two trials.

¨  Forecasting Reliability - For three trials (k' = 3)

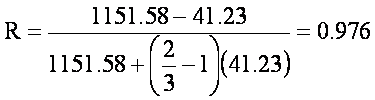
¨  Interpretation - The reliability for the test if three trials were administered, the reliability would be 0.976, slightly higher than for two trials (0.964).

n   Application of Forecasting

¨  The forecasting method can be used to develop a testing protocol.

¨  In the example just illustrated, the reliability of a 2-trial test was very high. This analysis showed that just using a single trial would result in only a small loss in accuracy.

¨  The method can also be used to determine how many additional trials would be required to improve reliability.

n   The Spearman-Brown prophecy formula is a second method that can be used to forecast test reliability.

¨  This method estimates the increase in test reliability for a test that has been lengthened by k times (k = 2, the test is twice as long, k = 0.5, the test is half as long, etc.).

¨  The reliability of test can be estimated for a longer test. The Spearman-Brown equation is:

             where r_1,1 is the computed reliability of the test, k is times the test is lengthened, and r_kk is the estimated reliability for the test lengthened k times.