PEP 6305 Measurement in
Health & Physical Education
Topic 4: Measures
of Variability
Section 4.1
n
This Topic has 1 Section.
Reading
n Vincent
& Weir, Statistics in Kinesiology 4th ed.,
Chapter 5 “Measures of
Variability”
Purpose
n
To discuss and demonstrate various measures of variability in a
distribution of scores.
Variability
n
Variability is an indicator of how widely scores are
dispersed around the measure of central tendency.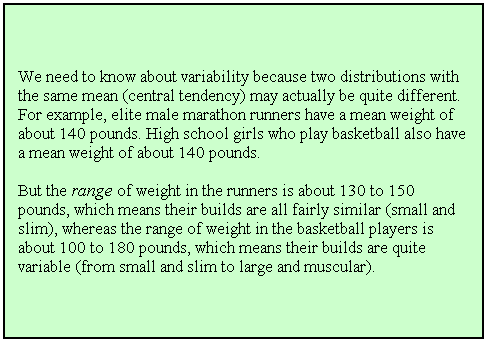
¨
Example: the GRE quantitative and verbal sections range
from a high score of 800 to a low score of 200. This spread of scores is one
indicator of the variability of GRE scores.
¨
Does a
leptokurtic or platykurtic distribution have a larger relative variability
about the central score? Can you sketch a line drawing of these distributions
that shows why?
n
A distribution is described by both its central value and its
variability.
¨
Reporting both measures is necessary to characterize the
distribution of data appropriately.
¨
When central tendency and variability are
known, different sets of data can be compared—which is a big deal in statistics.
n
Generally, four indicators of variability are used: range,
interquartile range, variance, and standard deviation.
Range
n
The range is the difference between the highest and lowest
scores.
¨
The picture at the right shows the tallest (7' 6" Yao Ming) and
shortest (5' 5" Earl Boykins) NBA professional basketball players from the year
2006.
¨
The range of heights of NBA players in 2006 was therefore 90
inches - 65 inches = 25 inches, or 2 feet 1 inch (looks like more than that,
doesn't it?).
n
The range can change dramatically with a change in either the
highest or lowest value (what would the range be if Boykins was released in
mid-season and the second shortest player was 5' 10"?
Answer).
n
The range is thus not a stable measure of variability, but can
give a rough indication of how scores are dispersed.
Interquartile Range
n
The interquartile range is the difference between
the scores at the 75th and 25th
percentiles (top
of
Q3 –
top of Q1).
Half of the scores in the distribution lie in the interquartile range. (Why?)
n
The interquartile range is
more stable than the range
because the
extreme values
(highest and lowest)
are
not part of its computation.
Thus, the extreme values can change by very large amounts, but the interquartile
range will likely be unaffected.
n
The interquartile range is used for ordinal data, or to describe
the variability of highly skewed interval or ratio data (Why?).
Population Variance
n
The variance uses deviations (d), or the difference
between each score and the
mean, to
compute an indicator of variability.
¨
The idea is that all of the d's can be combined to compute
the average deviation; the average distance between the mean and the scores.
n
The sum of the deviations for any set of data is 0 (∑d = 0;
see Table 5.1). So we cannot use the sum of the deviations as an indicator of
variability.
n
Instead, we sum the squares of the deviations; this takes
care of the “sum to zero” problem, because the sum of the squared deviations
will not sum to 0 (∑d2 > 0).
n
To normalize the sum of squared deviations ( ∑d2
), divide by the number of scores (N). The resulting value is the
variance (V):
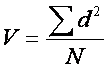 The
variance may also be symbolized by σ2 (population parameter).
[σ is the lowercase Greek letter sigma]
The
variance may also be symbolized by σ2 (population parameter).
[σ is the lowercase Greek letter sigma]
Population
Standard
Deviation (Parameter)
n
The measurement unit for variance is the squared measurement unit
of the original variable. This makes it difficult to interpret and compare
between variables; it would be easier if the indicator of variability was in the
same unit as the original variable. 
n
The solution is easy enough: take the square root of the variance.
n
This value is called the standard deviation (σ)
because it is the average deviation in the same unit as the original variable;
this is what we set out to find.
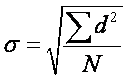
n
This formula can be unwieldy in large data sets, so a
user-friendly formula is provided that requires only the square of each score
and the mean:
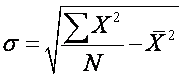
n
Of course, you would just use a computer to calculate the standard
deviation, right? Yes—except that statistical programs compute a
sample standard deviation, not the population parameter standard
deviation.
¨
If for some reason you have all of the data in the population, you
would use one of the formulas above to calculate the parameter value.
¨
This would be very unusual. In the vast majority of cases you
would be interested in computing the…
Sample Standard
Deviation (Statistic)
n
When a sample is used to calculate a value rather than using the
entire population, it always underestimates the population value. Thus,
the formula for computing the sample standard deviation has a built-in
adjustment to account for the underestimation.
n
The adjustment brings attention to a very important statistical
concept: degrees of freedom (df). The “degrees” part means a
number that is a count of something (subjects, groups, etc.). The “freedom” part means the number of values in the data that are “free
to vary.”
¨
Free to vary means that when one statistic is calculated
using another statistic, the amount of information used to make the calculation
is limited--you have less information for the second statistic than you did for
the first because you used some of that information in computing the first
statistic.
¨
So, since the sample standard deviation (a statistic) uses the
sample mean (also a statistic) in its calculation, the information is limited.
The information is limited because you have used some of the information in the
data to estimate the mean.
¨
The example given on page 65 of the text demonstrates the
df concept.
If there are four scores, and the computed (sample) mean is 5, then (using the
formula for computing the mean) the sum of the four scores must be 20. Why? 
¨
Recall from
Topic 3,
the formula for the mean: 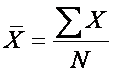 .
.
¨
If you rearrange the terms, the sum ( ∑ X ) =
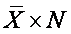 .
So: Sum = 5 (mean) x 4 (N) = 20.
.
So: Sum = 5 (mean) x 4 (N) = 20.
¨
What
this means is that if both N and 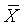 of
a sample is known then the sum is determined (i.e., known).
of
a sample is known then the sum is determined (i.e., known).
¨
Consequently, if you know the sum of four values, and you know any three
of the values, then the fourth value is “not free to vary.”
¨
Thus,
there are only 3 “degrees of freedom” in this example.
n
The adjustment to the formula for the sample standard deviation
(SD) involves dividing the sum of the squared deviations by the degrees of
freedom, which is the sample size (N) minus 1 (you subtract 1 because you
used that information to compute the mean):
Definitional formula: 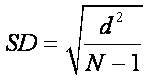 ,
and computational formula:
,
and computational formula: 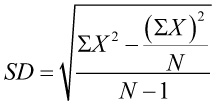 (the computational formula is easier when computing by hand,
because all you need is the sum of the scores and the sample size).
(the computational formula is easier when computing by hand,
because all you need is the sum of the scores and the sample size).
n
As stated above, you would usually use a computer program such as
R Commander to calculate the SD.
n
In a normal distribution, there are about 3 SD between the mean
and the highest score, and about 3 SD between the mean and the lowest score, for
a total dispersion (range) of scores of about 6 SD, as shown in this figure:

n
Most of the values in the normal distribution (under the
red
curve) are within ±3 SD of the mean (the blue
line at SD = 0). Very few scores exist beyond 3 SD on either side of the mean.
n
In the next Topic, we will discuss how to use the standard deviation and its
relation to the normal distribution.
Formative
Evaluation
n
Compute by hand the SD for these by-now familiar
data:
525, 505, 507, 654, 631, 281, 771, 575, 485, 626, 780, 626. What is the range of
these data? What is the interquartile range? (Answers)
¨
Compute the SD using R Commander. Enter the data in a blank New
data set. Go to Statistics>Summaries>Numerical summaries… Click to highlight the variable
in the Variables box, click OK. An
output file shows the mean, SD, and quantile values.
¨
Your hand-computed values and R Commander values for mean
and SD should be the same.
n
Open your data file in R Commander and compute the mean and SD of age, ht
(height in cm), wt (weight in kg), bmi (body
mass index), pfat (% body fat), and afit (aerobic fitness). What is
the median and range of each variable?
n
Tables are an efficient way to present descriptive data. Make a
table summarizing your the data in your data file. Put the names and units
of measurement for the variables in the left column. In the top row, put the
name of the statistic being reported. Tables should be numbered, even if there
is only one table, and should have a title. Your final table should look
something like this (except with your data file's actual numbers):
Table 1.
Characteristics of the study sample (n = 1000).
|
Variable |
Mean |
SD |
Range |
|
Age (yr) |
50 |
10 |
20 – 80 |
|
Height (cm) |
50 |
10 |
20 – 80 |
|
Weight (kg) |
50 |
10 |
20 – 80 |
|
BMI |
50 |
10 |
20 – 80 |
|
Body fat (%) |
50 |
10 |
20 – 80 |
|
Aerobic capacity
(mlO2/kg/min) |
50 |
10 |
20 – 80 |
SD = standard deviation.
BMI = body mass index.
n
In other types of tables, the columns might represent groups of
subjects or time intervals (before and after, for example). Alternately, a table
can have one or two of the independent variable as rows and the other variables
in the columns.
You have reached the end of Topic 4.
Make sure to work through the Formative Evaluation
above and the textbook problems (end of the chapter).
(remember how to enter data into R Commander?)
You must complete the review quiz (in the Quizzes
folder on the Blackboard course home page) before you can advance to the next topic.


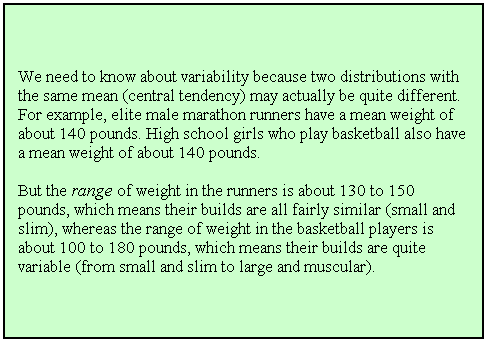

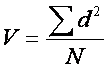 The
variance may also be symbolized by σ2 (population parameter).
[σ is the lowercase Greek letter sigma]
The
variance may also be symbolized by σ2 (population parameter).
[σ is the lowercase Greek letter sigma]
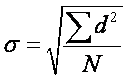

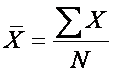 .
.
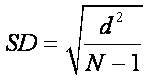 ,
and computational formula:
,
and computational formula: 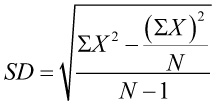 (the computational formula is easier when computing by hand,
because all you need is the sum of the scores and the sample size).
(the computational formula is easier when computing by hand,
because all you need is the sum of the scores and the sample size). 